苹果叶片病害多标签分类
|
|
前言
一个做的有点烂烂的小作业,主要是还是十分的新手,什么都不太懂,也不知道改什么好怎么改好,就把几个模型套壳拼接了一下,总的来说FPN在这里是没有发挥出来什么作用的,但是它的可视化比较好看所以就放进来了。
分类任务来自Kaggle,Plant Pathology 2021 - FGVC8
- Swin-Transformer主要代码参考WZMIAOMIAO/deep-learning-for-image-processing其中的ST模型实现;
- Query2Label主要代码参考curt-tigges/query2label的模型实现;
- FPN主要代码没有参考了,手搓了。
其实比较简单的Swin-Transformer加上Query2Label就可以获得很好的效果的,确实没必要加上FPN,显存完全不够用,但是这是要卷的作业,就表示一下曾经尝试过吧。
所有代码已经开源,详见lankoestee/Plant-Pathology-2021。
问题简介
相关任务
图像分类问题一直是计算机视觉中的基础问题,尤其是图像分类中的细粒度分类问题,其具有类内差异大,类间差异小的特点。自从卷积神经网络(CNN)面世之后,使用深度学习方法进行图像分类就成为了目前的常用方法。2014年,深度卷积神经网络VGG的出现更是大幅提高了图像分类的准确度,随后,resnet网络的出现同样在一定程度上提高了其性能,但是日渐增大的网络结构限制了其的进一步发展和应用。
2017年,Transformer结构首次应用在了自然语言处理(NLP)上,其使用了多层的自注意力机制和前馈神经网络来进行信息的处理和转换。自注意力机制通过计算一个注意力权重矩阵,将输入序列中的每个位置与其他位置进行交互。这种交互使得Transformer能够更好地理解序列中的上下文关系,并且能够并行计算,加快了训练和推断的速度。
作为Transformer结构在NLP之外的重要推广,Vision Transformer是一种基于Transformer的图像分类模型,它将图像像素作为输入,通过一系列的Transformer编码层来提取图像中的特征,并最终进行分类。与传统的基于卷积神经网络的图像分类模型不同,ViT直接将图像分割成一系列的图像块,并将每个图像块作为输入序列传递给Transformer编码器。这样做的优势是可以处理任意大小的图像,并且能够捕捉到全局的上下文信息。
然而,由于ViT在处理大尺寸图像时存在计算和内存消耗过大的问题,为了解决这个问题,2021年提出了Swin Transformer。Swin Transformer采用了层次化的注意力机制,将图像分割成不同的窗口,并在不同层级上进行特征交互。这种层次化的设计使得Swin Transformer能够在处理大尺寸图像时具有较低的计算和内存需求,同时保持了较好的分类性能。
Vision Transformer和Swin Transformer的出现使得Transformer模型在图像分类领域得到了广泛的应用和探索。它们证明了Transformer不仅在自然语言处理领域取得了成功,也可以在计算机视觉任务中取得令人满意的结果。这为解决细粒度分类等图像分类问题提供了新的思路和方法。
本次任务
Plant Pathology-2021是Kaggle举办的FGVC8(CVPR2021-workshop)的数据集,任务是对叶片的病害进行分类,共有3651张RGB图片。其属于一个细粒度分类问题,数据集的拍摄主体都是苹果叶片,由于光照和拍摄角度的原因,其类内差异巨大,类间差异却很小,主要的判断角度是叶片中会出现的黄色斑点和叶片形态不同。此外由于同类病害的栽培环境不甚相同,并且环境存在较大的差异,这也为该问题增加了难度。
作业的难点在于植物病理学图像的复杂性,包括不同的病害类型、病害的严重程度和叶片的外观变化。同时该任务具有一个显著特征,即并非传统的单标签分类问题,而是一个多标签的分类问题,也就是同一个叶片可能会同时具有1种或多种形态,归属两类不同的病害,这也将会为后续的处理带来一系列的挑战。
相关任务
Swin-Transformer
Swin-Transfomer所对标的工作是第一个将Transformer结构使用于计算机视觉领域的Vision Transformer。相较于Vision Transformer对于个图像区域进行自注意力机制,其复杂度为,Swin Transformer采取了分治的方法,如图3所示,也就是将N个图像区域进行固定常数的拆分,也就是拆成了组,每组个图像区域及逆行计算,其整体复杂度变为。但由于是一个常数,故该复杂度即为,这大幅降低了自注意力机制的复杂度。
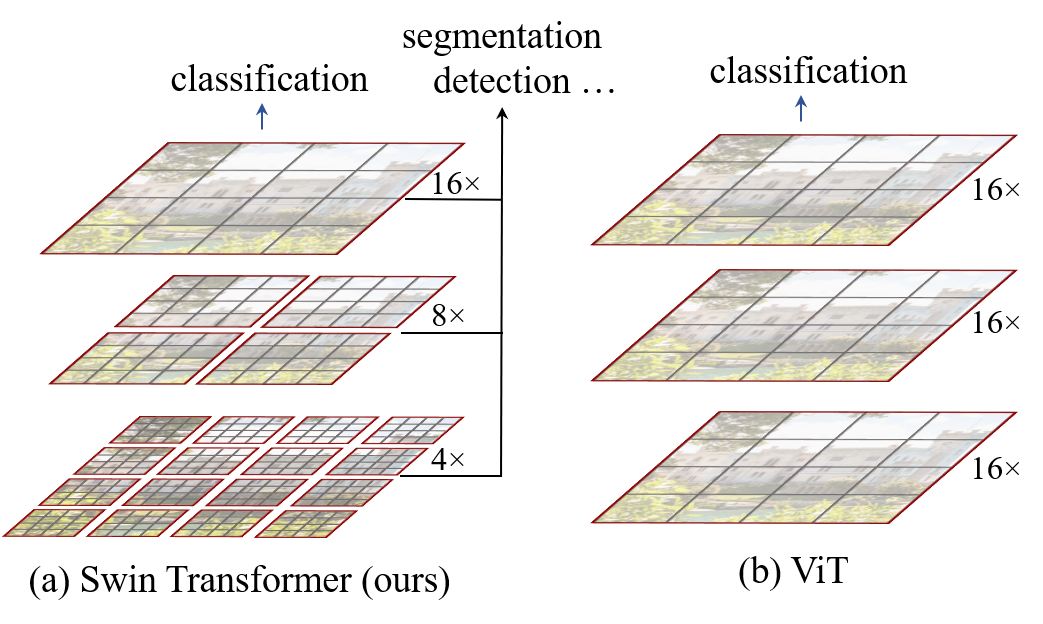
但这样所带来的结果便是各个区域之间无法做到信息的交互,这对于图像分类问题而言是致命了,故在论文中,其采用了更加滑动窗口(Shifted Windows)的办法完成信息在不同窗口之间的交互,如图4所示。Swin Transformer将分隔窗口(Window Partition)整体向右下角移动一定单位,并将分割窗口外左上角的图像区块平移至了右下角进行补充。这带来了一个问题,即在满足了图像交融任务的同时,将原本没有物理关系的图像区块粘合到了一起。为此,该模型建立了带有掩膜的多头自注意力机制(Masked MSA),在计算存在粘合区块时,将没有物理关联的区块使用掩码掩盖,实际操作上就是赋予特定值(-100.0),使之无法参与梯度计算。
对于其主干网络架构(backbone),将会在后续进行阐述。
Query2Label
Query2Label是2021年清华大学提出的一种简单的适用于多标签分类的方法,具有极好的性能,在诸如PASCAL VOC等数据集的多标签分类任务上均拿到了mAP第一的成绩。
对于从单标签分类问题到多标签分类问题的常用方法,便是使用Sigmoid激活函数和BECLoss的损失函数进行改进。而实际上,其多标签分类任务存在两个明显的难点,一是如何处理标签数量差异带来的类别不均衡问题,二是如何区分不同兴趣区域的特征。
Query2Label将同样也将Transformer运用于了分类任务中,其作为一个二阶段(two-stage)的解决方案,将其第一阶段为可以替换的主干网络,可以接入VGG,ViT的等基于卷积神经网络或Transformer的模型。在第二阶段上,Q2L将图片特征和标签特征一起送入Transformer解码器中,图片特征作为键(key)和值(value),标签特征作为查询(query),将Transformer输出的查询特征经过自适应特征池化和线性投影后预测标签存在性,如图5所示。
在Q2L的Transformer解码器中,每一层的解码器都采用了一个自注意力模块(self-attn),一个交叉注意力模块(cross-self)和一个带位置编码的前馈网络。
对于特征池化和线性投影而言,可以使用全局平均池化(GlobalAvgPool)和全连接层(FC)进行实现。
FPN
特征金字塔(FPN, Feature Pyramid Networks)是2016年由Facebook研究院提出的一种进行目标检测的方法,也可以拓展到图像分类方面,传统的算法都仅由图像的最高层进行预测与分类,最高层的特征图语义信息丰富,但是具体内容较少,较低层的特征图语义信息较少,但是具体内容多。FPN网络在传统网络自下向上的连接方式之后,进行了自上而下的连接。
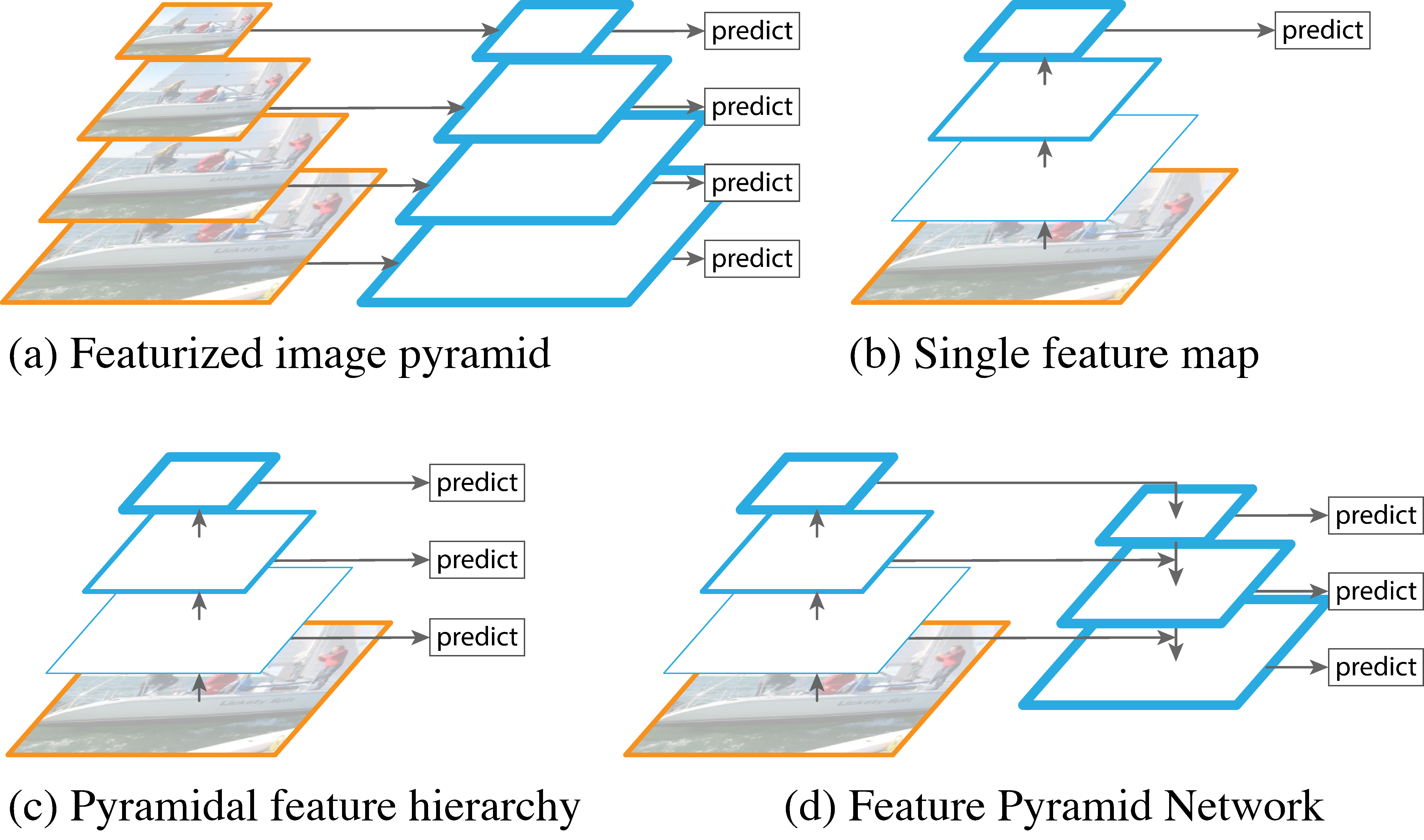
从图6中可以看出,相较于传统的单特征预测以及使用每个特征进行预测,FPN网络在没有增大太多数据量的情况下实现了上层语义信息和下层实际信息的交互融合,并使用了多个特征图进行特征预测。该结构最早应用在了目标检测的Faster-RCNN中,取得了较好的效果。在FPN网络自上而下的特征图连接中,其均使用了较为简单的方法。横向连接中,左侧特征图通过一个卷积便来到了右边,而自上而下的连接中,上层的图形通过上采样(upsampling)方法便可以达到与下层特征图相同的尺寸,便于直接进行加和操作。
针对本细粒度问题而言,FPN通过在不同尺度上构建特征金字塔,提供了多尺度的特征表示。在图像分类任务中,FPN可以通过将不同尺度的特征图结合起来,获得更全局和更细粒度的特征表示,从而提高分类模型的性能。具体来说,FPN通过自上而下的特征传播和自下而上的特征融合,将来自不同尺度的特征图进行融合和整合。这样可以使网络在处理细粒度问题时能够同时关注到全局特征和局部细节,从而提高分类的准确性和鲁棒性。
数据处理
图像处理
在Plant Pathology-2021的数据集中,叶片图像的分布并不是无迹可寻的,找出其中存在的特点有利于进行后续的相关训练,通过在训练集上的图像通读,不难发现其图片的排布存在如下的几个特点。
- 叶片多呈现横向舒展,而较少呈现纵向的舒展,并且叶尖朝向存在向左或向右的可能;
- 叶片基本集中在画面的中央,四周的画面大多不是该叶子的图像;
- 图片的格式不同一,没有固定的大小。
基于以上三点,我们可以对图片进行以下的处理
- 随机进行水平方向的反转,以防止左右朝向的不均衡;
- 进行中心裁剪,仅保留中心叶片,而去除周围环境;
- 缩放并标准化图像数据。
上述的图像简单处理过程可以在图2中进行展现。才将过后,图像所代表的叶片没有被大幅度裁剪,但是周围环境在其中的占比被明显降低了。也就是内容的含量得到了提高
标签处理
对于该问题的训练集而言,其共有12个分类,但是部分分类存在重合的情况,也就是一个图像对应了多种病害,独立的病害种类仅有6种。由于其标签排列组合出来的种类不多,我们固然可以使用12类的单标签分类进行本次任务的处理,但是这将再次减少我们的类间差距,使得原本较小的内类差距更小,这是所不希望看到的。故于此,本人的模型仍然采用了多标签分类的方法,也就是将其转化为独热编码(one-hot)。与单标签问题的独热编码相不同的是,多标签分类中的独热编码不仅只有一个值为1,而是允许多个值为1,图2是部分独热编码的示例。
通过类似于此的独热编码,我们可以将图片映射到6个值上去,以作为计算损失函数的一个标准。
模型建立
下文所提到的两个模型均是经过本人修改实现的模型,虽然最终的效果未见得好,但是网络上均没有相关的理论和应用案例,尤其是Swin Transformer和FPN的结合,以及Query2Label在自定义数据集上的实现。
Query2Label on Swin Transformer (QST)
Swin Transformer相对于Vision Transformer,其具有一些类似于CNN网络的特征,也就是呈现出一个线性排列的特征。对于进行多标签分类的Query2Label而言,网络上暂未出现较为通用的复现方案,主要原因是大部分的模型都是针对MS-COCO数据集的相关代码,同时使用timm来对主干网络进行包装,这不方便我们的使用。故在此,本人将Swin Transformer与Query2Label进行了源码层面上的结合,其结合后的网络结构如图7所示。
在图7的Swin Transformer Backbone部分,包含了一个最为基础的Swin Transformer结构,共有四层Swin Transformer Block,每个Block不会改变输入和输出的特征图维度大小和通道大小,即输入多大输出多大。而实现特征图融合和通道增加的步骤是图像拼接(Patch merging),其通过将图片裁剪为四块并拼接,使得图像从的形状变为的形状,通过层正则化(Layer Normalization)的手段和在通道维度上的一个简单的全连接层将特征图变为的形状,减少后续计算量。
图7所示的Swin Transformer Block配置是最为基本的tiny配置,四层Block的自注意力机制分别为。在不同大小的模型中,这是可以被改变的,而其中的数量必须为偶数,因为每组自注意力机制是由一个多头自注意力(MSA)和一个基于窗口的多头自注意力(W-MSA, Window-based Multi-head Self-Attention)。MSA即为传统的自注意力机制,而W-MSA则是结合了图2中所示掩码的自注意力机制。两者的组合在减小计算量的保证了各个窗口之间的信息交互,在最基本的Swin Transform架构中,窗口的大小为7。
在后续的Query2Label架构中,首先使用了一个conv 1x1对前面生成的特征图进行了维度上的改造,其类似于一个全连接层,但是有效地把原有的通道大小降低到了,在基本的Swin Transformer配置中,,这样的通道维度还是过大的。由于transformer仅能够接受一维的顺序数据,故于此,我们必须将图片数据进行展平操作,该操作同样也是经历多步的维度变换的。将展平后的数据送入多个transformer解码器后,将其输出通过一个线性层,便得到了最后的预测类别。在基础的Query2Label设置中,transformer解码器的个数为6个。
Query2Label on Feature Pyramid Swin Transformer (QPST)
除了建立基于Swin Transformer和Query2Label结合的模型之外,本人还尝试将FPN网络使用到本人的模型中来,其主要原理便是在Swin Transformer的backbone上进行更改,获取其每一个阶段(stage)后所得到的特征图,通过FPN的多特征融合,最后送入Query2Label的多标签处理变换器。其模型架构图如图8所示。
如图所示,整个网络由3个部分组成,分别是作为主干网络的Swin Transformer,其依然是可以更改的,也就是可以控制其中的MSA以及W-MSA模块个数,在图8中是其最为基本的版本,也就是。随后是包含了整个主干网络的FPN网络部分,其核心在于通道变换的卷积、的上采样以及的特征融合卷积。在这里本人对传统的FPN网络进行了一点点的调整,即FPN网络的最顶特征图,图4中的最顶特征图将不会单独传入后续处理步骤中,而是会融入下层信息,但其中具有最高的语义信息,不直接使用由些许的浪费,故本人也将其送入了Query2Label的处理步骤中。经过FPN网络后,即是基本配置的Q2L网络,通过transformer的处理后,将其信息进行平均以及归一化后,便可以得到最终的预测labels。
上述的模型结合了FPN进行多尺度特征图融合的良好能力,可以有效的增加其感受野,并将与实际相关的信息更好的融合在了一起。同时,图8中也对其每个阶段后的特征图大小进行了标记。需要注意的是,在卷积部分,由于为了后续实现上采样的融合,需要将不同通道数的特征图转化为具有相同的通道,对于上层的特征图而言,其较小图幅面积对于通道的变化不会产生较大的计算量。而对于下层的特征图而言,较大的图幅面积以及较大的通道数,可能会产生较大的计算量,这是我们后续要进行分析的。
模型训练
损失函数
损失函数(Loss function)是用来衡量模型预测结果与真实结果之间的差异的函数。它通常用于机器学习和优化算法中,通过最小化损失函数来调整模型的参数,使模型能够更好地拟合训练数据。对于单标签的二分类任务,交叉熵、对数损失函数都是一些常用的损失函数,但是对于多标签问题而言,损失函数的选择就变得不同了。本叶片分类问题总共有6个类,且每个类的正例和负例个数不尽相同,譬如scab类有较多的正例,而powdery_mildew仅有很少一部分正例。如图9所示,以训练集为例,所有类均是正例较少而反例较多,故给损失函数的选择造成了一定的困难。
二元交叉熵损失(BCEWithLogitsLoss)
常见的损失函数,如BCEWithLogitsLoss,它将Sigmoid层与BCELoss合并成了一个损失函数,在多标签分类的情况下,其损失函数可以被描述为
其中为类别总数,为第个类别的损失函数、表示第个样本在第个类别上的损失,表示第个样本在第个类别上的权重,表示第个类别的先验概率。该损失函数十分方便使用,能够有效处理多标签分类问题,并直接优化预测结果,但是对于图9所示的类别不均衡问题,其并不能显示出较好的性能,或是说相差性。本人曾尝试是使用,但取得了不好的效果。
不对称损失(AsymmetricLoss)
AsymmetricLoss是一种用于解决类别不平衡问题的损失函数。它在二分类问题中被广泛使用,特别适用于当正负样本比例严重不平衡时。自然的,其可以被用于多个类别的二分类任务。
AsymmetricLoss的特点是对正负样本进行了不对称处理,即对正样本和负样本的损失权重进行了不同的设定。它的目的是通过调整损失函数中正负样本的权重,使得模型在预测时对少数类别更加关注,从而提高模型在少数类别上的性能。
AsymmetricLoss是一种结合了二元交叉损失(BCE),FocalLoss的损失函数,其计算方式如下
相较于传统的FocalLoss仅有一个参数而言,AsymmetricLoss将其变为了和两个参数,分别代表了正样本和负样本的不对称系数,也就是权重。通常来说,AsymmetricLoss中正样本的权重会设置得比负样本的权重高,这样可以使得模型在正样本上的预测更具有决定性。我们采用了一般的通用设计,也就是、。这种不对称处理可以有效地应对类别不平衡问题,提高模型在少数类别上的召回率和准确率。这也如图9所示,能够正好对应我们的数据集。在后续的训练中,本人使用了这种损失函数。
附加角度裕度损失(Arcface Loss)
Arcface Loss是一种用于人脸识别任务的损失函数。它是通过将特征向量映射到一个高维的球面空间来实现人脸特征的判别性学习。Arcface Loss使用角度余弦作为相似度度量,旨在增加同一类别之间的相似度,同时增加不同类别之间的差异度。其损失函数的计算公式如下。
Arcface Loss的核心思想是引入一个额外的角度余弦因子也就是上式中的,在特征向量与类别嵌入权重之间进行调整。通过对角度余弦进行缩放和偏移,可以增强特征向量的判别能力。具体而言,Arcface Loss在Softmax分类器的基础上引入了一个角度余弦余弦因子,将特征向量与类别权重进行缩放,使得同一类别的特征向量更加接近,而不同类别的特征向量更加分散。
通过使用Arcface Loss作为训练过程中的损失函数,可以提高人脸识别任务的性能。类似的由于本任务为叶片分类任务,与人脸识别任务有诸多的相似之处,都是在整体近乎一致的情况下进行细粒度的区分,故理应能够优化其性能。
优化器
adam优化器
Adam优化器是一种在深度学习中常用的优化算法之一。它结合了自适应矩估计(Adaptive Moment Estimation)和RMSProp算法的优点,具有较好的性能和收敛速度。
Adam优化器通过自适应地调整每个参数的学习率,根据梯度的一阶矩估计(均值)和二阶矩估计(方差)来更新参数。它能够在训练过程中自动调整学习率,对于不同参数具有不同的学习率,从而更好地适应不同的数据和模型。
相比于传统的随机梯度下降(SGD)等优化算法,Adam优化器通常能够快速地收敛到较好的局部最优解,并且对于超参数的选择相对较少敏感。然而,在某些情况下,Adam优化器可能会导致模型陷入局部最优解或者在训练初期过度调整学习率,从而影响模型的性能。
总体而言,Adam优化器在深度学习中被广泛使用,但并不适用于所有情况。在具体应用中,需要根据问题的特点和实验结果来评估和选择最适合的优化算法。
adamw优化器
AdamW优化器是对Adam优化器的一种改进版本。AdamW的"W"代表权重衰减(Weight Decay),它在Adam的基础上加入了权重衰减项,用于对模型的参数进行正则化。
AdamW优化器的主要区别和优点如下:
- 权重衰减:AdamW通过引入权重衰减项,可以有效地对模型的参数进行正则化,防止模型过拟合并提高泛化能力。
- 正则化效果改进:相比于Adam优化器,AdamW可以更好地控制模型的正则化效果,减少权重衰减对学习率的影响,从而提高优化的稳定性和性能。
- 学习率的修正:AdamW对Adam中的学习率进行了修正,使其在训练初期更加平稳,减轻了学习率的过度衰减问题。
- 收敛速度:在某些情况下,AdamW优化器相比于Adam优化器可以更快地收敛到较好的局部最优解,提高了训练的效率。
据此,本人使用了adamw优化器作为后续训练的优化器,其中weight-dacay参数的设置较难把握,设为较好。
学习率调度策略
通常而言,将学习率设置为一个固定的值,如或等数即可,但是为了更快的使模型收敛和提高泛化能力,pytorch提供了一些方便使用的学习率调度器
OneCycleLR
OneCycleLR是PyTorch中的一个学习率调度器(learning rate scheduler)。它实现了一种称为"One Cycle"的学习率调度策略,旨在在训练过程中动态调整学习率,以加快模型的收敛速度和提高泛化能力。
One Cycle学习率调度策略的核心思想是在训练过程中逐渐增加学习率,然后再逐渐减小学习率。这样的学习率变化模式可以帮助模型在训练初期更快地收敛,并在训练后期避免过拟合问题,其大致的学习率-步数曲线如图10所示。
具体而言,pytorch中提供的optim.lr_scheduler.OneCycleLR通过设定初始学习率、最大学习率、学习率持续增加的步数、学习率持续减小的步数等参数,自动调整学习率的变化。在训练过程中,学习率会从初始值逐渐增加到最大值,然后再逐渐减小,形成一个完整的循环。
使用OneCycleLR可以帮助优化模型的训练过程,也是本人在后续训练中所选择的学习率调度器。
评价指标
在多标签分类任务中,macro和micro是两种常用的评价指标计算方式。
Macro指标是对每个类别分别计算指标值,然后对所有类别的指标值取平均。例如,对于每个类别的准确率,分别计算每个类别的准确率,然后将所有类别的准确率取平均。这种计算方式将每个类别都视为同等重要,不考虑类别之间的样本不均衡问题。
Micro指标是将所有类别的预测结果汇总起来,计算总体的指标值。例如,对于每个类别的准确率,将所有样本的预测结果汇总,计算整体的准确率。这种计算方式将所有样本都视为同等重要,考虑了样本不均衡的问题。
具体而言,对于多标签分类任务中的macro和micro指标,常见的计算方式如下:
-
Macro Precision(宏平均精确率):对每个类别计算精确率,然后取平均。
-
Macro Recall(宏平均召回率):对每个类别计算召回率,然后取平均。
-
Macro F1-score(宏平均F1分数):通过平均的precision和recall进行计算。
-
Micro Precision(微平均精确率):将所有类别的真阳性、假阳性和假阴性汇总,计算总体的精确率。
-
Micro Recall(微平均召回率):将所有类别的真阳性、假阳性和假阴性汇总,计算总体的召回率。
-
Micro F1-score(微平均F1分数):将所有类别的真阳性、假阳性和假阴性汇总,计算总体的F1分数。
结果展示
训练过程
在训练过程中,本人记录了验证集上的ValidLoss以及训练集上的TrainLoss,同时记录了其在训练集和验证集上的micro-mAP。对于图7所示的Swim Transformer + Quey2Label(QST)模型而言,其在训练集和验证集上的相关训练指标如图11所示。训练参数如表1所示。
| 训练参数 | Parameters | Value |
|---|---|---|
| 轮次 | epochs | 100 |
| 批次大小 | batch-size | 32 |
| 图像大小 | image-size | 256 |
| 学习率 | learning-rate | 0.0001 |
| 权重衰减 | weight-decay | 0.01 |
不难看出,随着训练轮次的增加,训练集损失显示出持续下降的趋势,而验证集在前65个轮次下降后保持了稳定,这说明训练此时产生了过拟合,没有得到较好的结果,过拟合是本次训练中存在的最大的问题。其损失和mAP如图12所示。需要注意的是,由于显卡性能的限制,加之租用服务器费用的限制,STPQ模型的图片大小仅为128,批次大小仅为8,这也可能导致训练过程的过拟合。
性能指标
由于QST和QPST模型训练的后期都出现了过拟合情况,故在最佳模型参数的选取上,均选取loss最小的最佳模型最为测试模型。对于QST模型而言,其在测试集上的mAP和F1-scores如图13和图14所示。
可以看到,其PR曲线和F1曲线都呈现出了一个较为正常的分布,mAP达到了0.82,最高的F1_score也达到了还可以的数值,即0.77。此外,上述所提到过的性能指标如表2所示。
| class | threshold | P | R | F1 | AP |
|---|---|---|---|---|---|
| scab | 0.668 | 0.734 | 0.800 | 0.766 | 0.879 |
| healthy | 0.782 | 0.898 | 0.786 | 0.838 | 0.926 |
| frog_eye_leaf_spot | 0.607 | 0.763 | 0.859 | 0.808 | 0.884 |
| rust | 0.659 | 0.878 | 0.942 | 0.909 | 0.958 |
| complex | 0.597 | 0.500 | 0.730 | 0.594 | 0.605 |
| powdery_mildew | 0.709 | 0.813 | 0.765 | 0.788 | 0.823 |
| macro-all | \ | 0.764 | 0.814 | 0.784 | 0.824(mAP) |
| micro-all | 0.675 | 0.792 | 0.806 | 0.799 | 0.824(mAP) |
对于QPST模型而言,由于其输入图像较小,自然无法达到QST-256所能做到的分类水平,其PR曲线以及F1曲线如图19所示,其性能指标如表3所示。
| class | threshold | P | R | F1 | AP |
|---|---|---|---|---|---|
| scab | 0.529 | 0.491 | 0.726 | 0.586 | 0.583 |
| healthy | 0.738 | 0.545 | 0.717 | 0.619 | 0.688 |
| frog_eye_leaf_spot | 0.464 | 0.473 | 0.796 | 0.593 | 0.563 |
| rust | 0.761 | 0.746 | 0.638 | 0.688 | 0.781 |
| complex | 0.516 | 0.389 | 0.333 | 0.359 | 0.414 |
| powdery_mildew | 0.709 | 0.36 | 0.53 | 0.429 | 0.353 |
| macro-all | \ | 0.501 | 0.623 | 0.546 | 0.564(mAP) |
| micro-all | 0.561 | 0.443 | 0.678 | 0.536 | 0.564(mAP) |
| QST-128* | \ | \ | \ | \ | 0.523(mAP) |
需要说明的是,threshold来自于验证集的最佳阈值,而非测试集,不会违背测试集仅用来测试的规则。
结果可视化
对于上述的QST模型而言,本人将其中各层的特征图进行了提取,对于多通道的特征图,本人将其进行了每个通道的平均处理,也就是将多个通道平均到一个通道上来,得到了如图15所示各环节特征图。
可以看到,尤其是第二幅图中,光照影响比较明显,反应到特征图中,就是在Path Partition和STstage1过后,仍然在相关的受光照位置,而在通过Swin Transformer的第二个block以后,相关的位置就不再与周围环境相迥异了,说明光照的因素在神经网络中被逐渐淡化。
对于QPST模型而言,由于其下采样的特征,其能够更加好的融合语义信息和广泛的特征,其各个环节,尤其是FPN环节的特征图如图17所示。可以看到,经过的融合卷积后,其特征图开始变的有意义了起来。尤其是卷积后最下层的特征图,本人将其作为掩膜,所得到功能类似于感兴趣区域(ROI, Region of Interest),如图18所示。可以看到,对于部分任务而言,尤其是关注其中的斑点而言,其确实能够起到重点关注的作用。
此外,针对多张不同类别的照片,通过两个模型的最佳模型文件,可以得到他们所预测出来的结果情况图16所示,可以看到,其对于scab、以及complex的预测容易出现些许的混淆,这是由于complex性状判断标准主观成分打所导致的。
总结与改进
在本次作业中,本人搭建了一个基于Swin Transformer和Query2Label的模型QST网络,以及将QST运用于FPN结构的QPST网络,并将其运用于Plant Pathology-2021的叶片分类问题,取得了较好的结果。但受限于显卡性能的限制,本人仅使用了Swin Transformer最基本的模型作为骨架,且在FPN和Q2L网络的参数选取上也选择的是最小的网络。在QST中,图像大小为256的训练输入取得了0.824的mAP。在QPST中,图像大小为128的取得了0.564的mAP,这主要是受限于硬件设置。
QST和QPST网络仍然存在诸多可以改进的地方,尤其是QPST网络。在其中的卷积部分,由于需要将所有特征图变换到相同的通道数,该通道数且不能太小,一般为256。对于下层最大图幅面积的特征图而言,这样的变化是十分耗费算力的,卷积的次数过大,卷积核过大,这也是硬件不支持图像大小为256的训练的重要原因。
