学习目的

区分相似和不相似的数据点，学习数据的表示，以捕捉不同数据点之间的基本结构和关系。

数据组成

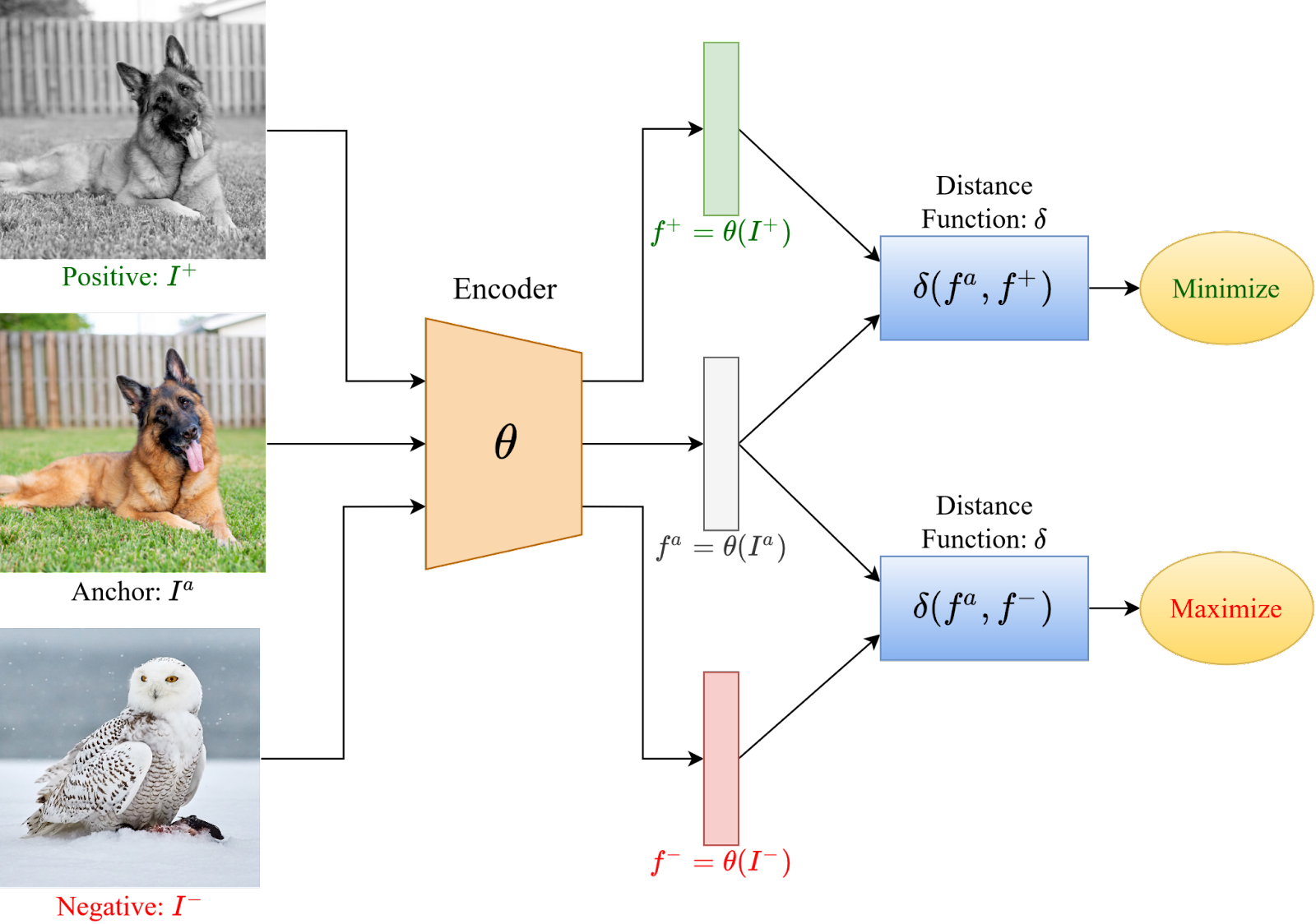
基本的对比学习框架包括选择一个数据样本，被称为“锚点”，一个与锚点属于相同分布的数据点，称为“正”样本，以及一个属于不同分布的数据点，成为“负”样本。学习的目标是在潜在空间中最小化锚点和正样本之间的距离，同时最大化锚点和负样本之间的距离。

损失函数

Max Margin Contrastive Loss

若不属于同一个分布，则最大化样本之间的距离，若属于同一分布，则最小化它们之间的距离。

Lconstrastive(si,sj,θ)=1[yi=yj]⋅∣∣θ(si)−θ(sj)∣∣22+1[yi≠yj]⋅max⁡(0,ϵ−∣∣θ(si)−θ(sj)∣∣22)L_{\text{constrastive}}(s_i, s_j, \theta) = \mathbb{1}[y_i=y_j]\cdot||\theta(s_i)-\theta(s_j)||^2_2+\mathbb{1}[y_i\neq y_j]\cdot\max(0, \epsilon-||\theta(s_i)-\theta(s_j)||_2^2)

这里的sis_i和sjs_j是需要比较的对应标签yiy_i和yjy_j的两个标签，θ\theta是嵌入网络，ϵ\epsilon是超参数，定义不同类别的样本之间的下界距离（也就是不要求不同分布样本之间的距离一直拉大，只要在ϵ\epsilon之外就认为它们已经完全分开了。

三元组损失

与上述的对比损失非常类似，但是同时以正样本、负样本以及锚样本的输入来计算损失。

Ltriplet=(sa,s+,s−,θ)=∑∀xmax⁡(0,∣∣θ(sa),θ(s+)∣∣22−∣∣θ(sa)−θ(s−)∣∣22+ϵ)L_{triplet} = (s_a, s_+, s_-,\theta) = \sum_{\forall x}\max(0, ||\theta(s_a),\theta(s_+)||_2^2-||\theta(s_a)-\theta(s_-)||_2^2+\epsilon)

与对比损失类似，没什么好说的，但是使用的比较多。

N-Pair Loss

N对损失是对三元组损失的扩展，不是对单个负样本进行采样，而是对N个负样本、一个锚点以及一个正样本进行采样，也就是扩展了采样的东西是什么，还是比较好理解的。

LN−pair(sa,s+,{si−}i=1N−1,θ)=−log⁡[exp⁡(θ(sa)T⋅θ(s+))exp⁡(θ(sa)T⋅θ(s+))+∑i=1N−1exp⁡(θ(sa)T⋅θ(s−))]L_{N-pair}(s^a, s^+, \{s_i^-\}_{i=1}^{N-1},\theta)=-\log\left[\frac{\exp\left(\theta(s^a)^T\cdot\theta(s^+)\right)}{\exp\left(\theta(s^a)^T\cdot\theta(s^+)\right)+\sum_{i=1}^{N-1}\exp\left(\theta(s^a)^T\cdot\theta(s^-)\right)}\right]

在一个批次的N个样本中，只有一个样本是与锚点同分布的正样本，其余的N-1个都是负样本。

NT-Xent损失

Normalized Temperature-scaled Cross Entropy Loss是对N对损失的修改，添加了温度归一化因子τ\tau参数，并使用余弦相似度计算相似度。

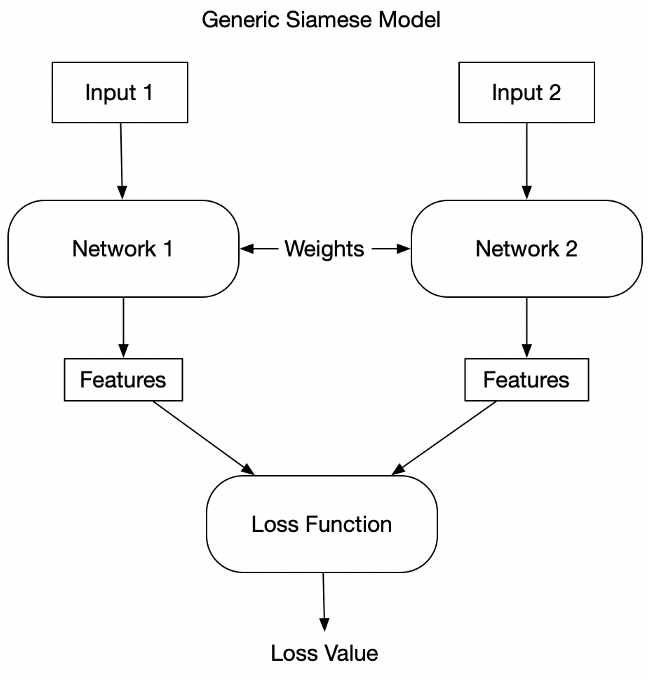
LNT−Xent(zi,zj)=−log⁡(exp⁡(sim(zi,zj)/τ)∑i=12N1k≠iexp⁡(sim(zi,zj)/τ))L_{NT-Xent}(z_i, z_j) = -\log\left(\frac{\exp(\text{sim}(z_i, z_j)/\tau)}{\sum_{i=1}^{2N}\mathbb{1}_{k\neq i}\exp(\text{sim}(z_i, z_j)/\tau)}\right)

这里的分母遍历对象是2N，因为在该损失中，对于一个批次的数据N，分别通过两个网络得到的结果，类似下面的这张图。其中的i和j分别是对应的，也就是ziz_i和zjz_j构成了一个正样本对，其余的都是负样本。

典型案例

现阶段而言最为典型的对比学习模型案例就是CLIP了，它做了一个图像和文本的对齐，在StableDiffsion3之前的诸多工作都是使用其作为文本编码器，以达到一个与图像对齐的效果。但是在后面的工作中，由于其较为有限的文本表达能力，目前更多使用T5作为文本编码器了，且T5没有进行对比学习。